RNN

2018-11-25 | 阅读：次

简介

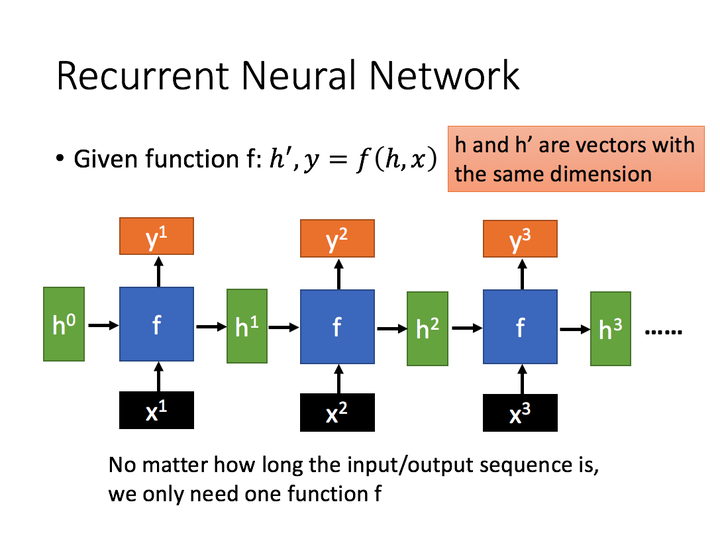
$x$ 为当前状态下数据的输入， $h$ 表示接收到的上一个节点的输入。

$y$ 为当前节点状态下的输出，而 $h'$ 为传递到下一个节点的输出。

通过上图的公式可以看到，输出 h’ 与 x 和 h 的值都相关。

而 y 则常常使用 h’ 投入到一个线性层（主要是进行维度映射）然后使用softmax进行分类得到需要的数据。

序列形式的表现，如下

LSTM

是一种特殊的RNN，主要是为了解决长序列训练过程中的梯度消失以及梯度爆炸问题。
相比普通的RNN，LSTM能够在更长的序列中有更好的表现

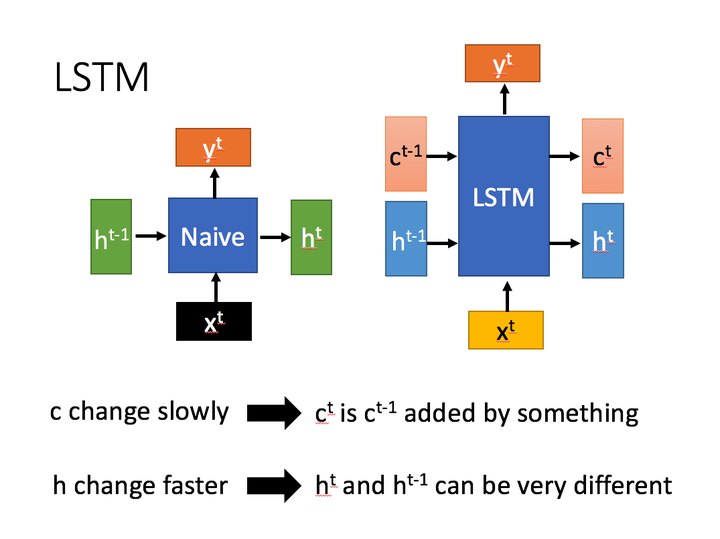
相比RNN只有一个传递状态 $h^t$ ，LSTM有两个传输状态，一个 $c^t$ （cell state），和一个 $h^t$ （hidden state）。（Tips：RNN中的 $h^t$ 对于LSTM中的 $c^t$ ）

其中对于传递下去的 $c^t$ 改变得很慢，通常输出的 $c^t$ 是上一个状态传过来的 $c^{t-1}$ 加上一些数值。

而 $h^t$ 则在不同节点下往往会有很大的区别。

深入LSTM结构

下面具体对LSTM的内部结构来进行剖析。

首先使用LSTM的当前输入 $x^t$ 和上一个状态传递下来的 $h^{t-1}$ 拼接训练得到四个状态。

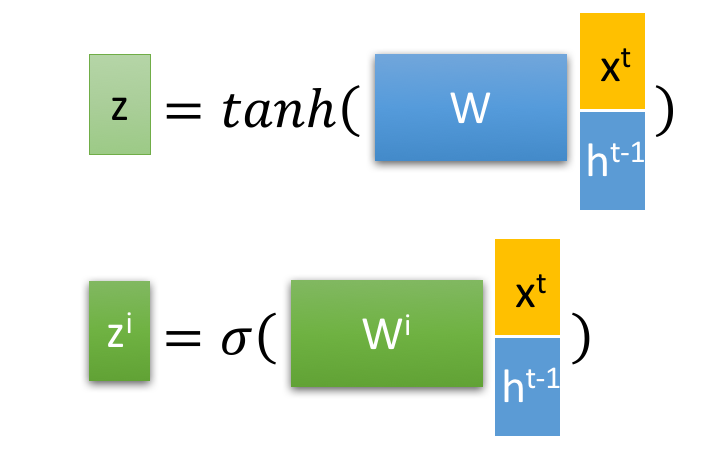
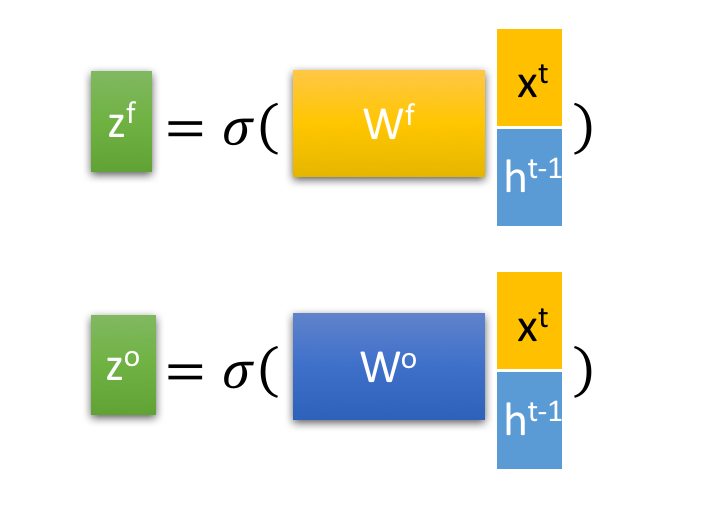
其中， $z^f$ ， $z^i$ ， $z^o$ 是由拼接向量乘以权重矩阵之后，再通过一个 $sigmoid$ 激活函数转换成0到1之间的数值，来作为一种门控状态。而 $z$ 则是将结果通过一个 $tanh$ 激活函数将转换成-1到1之间的值（这里使用 $tanh$ 是因为这里是将其做为输入数据，而不是门控信号）。

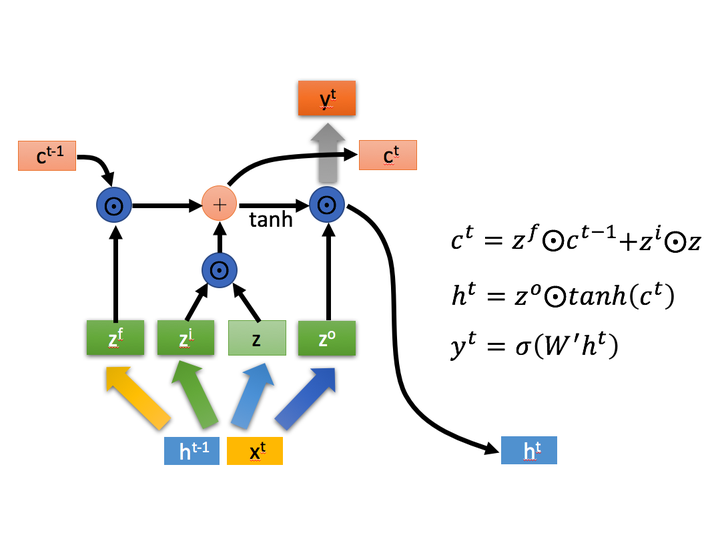
$\odot$ 是Hadamard Product，也就是操作矩阵中对应的元素相乘，因此要求两个相乘矩阵是同型的。 $\oplus$ 则代表进行矩阵加法。

内部三个阶段

LSTM内部主要有三个阶段：

\1. 忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的，记住重要的”。

具体来说是通过计算得到的 $z^f$ （f表示forget）来作为忘记门控，来控制上一个状态的 $c^{t-1}$ 哪些需要留哪些需要忘。

\2. 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入 $x^t$ 进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的 $z$ 表示。而选择的门控信号则是由 $z^i$ （i 代表information）来进行控制。

将上面两步得到的结果相加，即可得到传输给下一个状态的 $c^t$ 。也就是上图中的第一个公式。

\3. 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 $z^o$ 来进行控制的。并且还对上一阶段得到的 $c^o$ 进行了放缩（通过一个tanh激活函数进行变化）。

与普通RNN类似，输出 $y^t$ 往往最终也是通过 $h^t$ 变化得到。

这包括两个部分。首先，称为“输入门层”的S形层决定了我们将更新哪些值。接下来，tanh层创建一个新候选值C̃ t的向量，该向量可以添加到状态中。在下一步中，我们将两者结合起来以创建该状态的更新。

GRU

GRU（Gate Recurrent Unit）是循环神经网络（Recurrent Neural Network, RNN）的一种。和LSTM（Long-Short Term Memory）一样，也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。

优势

更容易进行计算

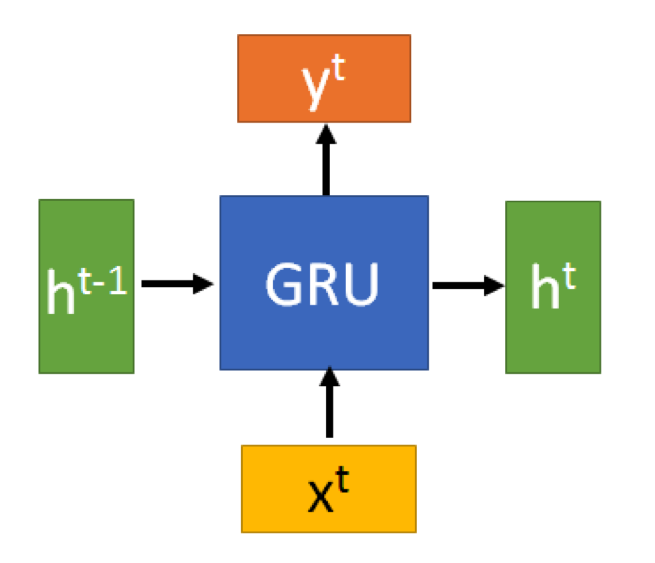
输入结构

GRU的输入输出结构与普通的RNN是一样的。

有一个当前的输入 $x^t$ ，和上一个节点传递下来的隐状态（hidden state） $h^{t-1}$ ，这个隐状态包含了之前节点的相关信息。

结合 $x^t$ 和 $h^{t-1}$ ，GRU会得到当前隐藏节点的输出 $y^t$ 和传递给下一个节点的隐状态 $h^t$ 。

内部结构

通过上一个传输下来的状态 $h^{t-1}$ 和当前节点的输入 $x^t$ 来获取两个门控状态。如下图，其中 $r$ 控制重置的门控（reset gate）， $z$ 为控制更新的门控（update gate）。

Tips： $\sigma$ 为sigmoid函数，通过这个函数可以将数据变换为0-1范围内的数值，从而来充当门控信号。

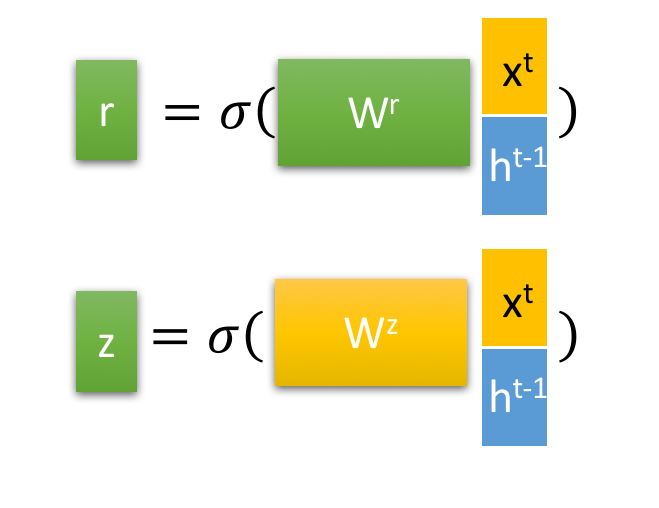
得到门控信号之后，首先使用重置门控来得到“重置”之后的数据 ${h^{t-1}}' = h^{t-1} \odot r$ ，再将 ${h^{t-1}}'$ 与输入 $x^t$ 进行拼接，再通过一个tanh激活函数来将数据放缩到-1~1的范围内。即得到如下图所示的 $h'$ 。

这里的 $h'$ 主要是包含了当前输入的 $x^t$ 数据。有针对性地对 $h'$ 添加到当前的隐藏状态，相当于”记忆了当前时刻的状态“。类似于LSTM的选择记忆阶段（参照我的上一篇文章）。

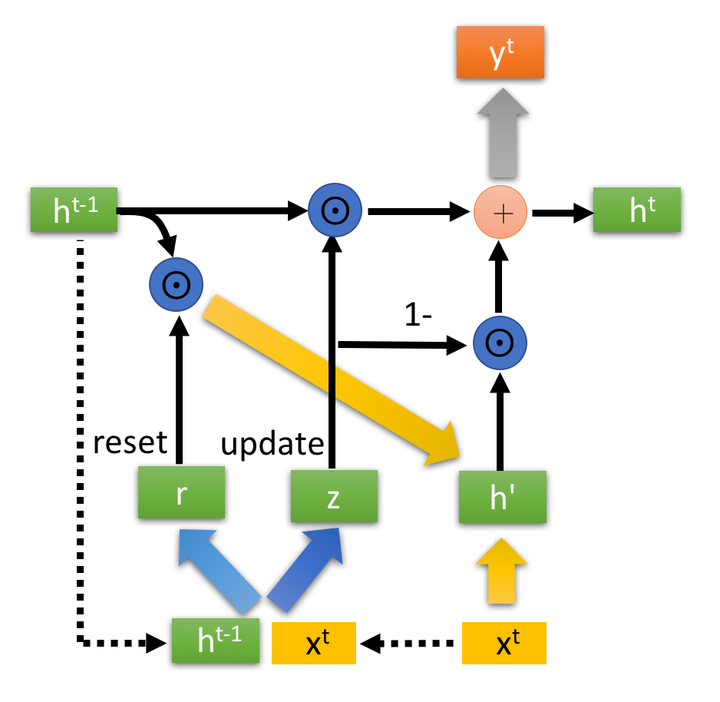
图2-3中的 $\odot$ 是Hadamard Product，也就是操作矩阵中对应的元素相乘，因此要求两个相乘矩阵是同型的。 $\oplus$ 则代表进行矩阵加法操作。

最后介绍GRU最关键的一个步骤，我们可以称之为”更新记忆“阶段。

在这个阶段，我们同时进行了遗忘了记忆两个步骤。我们使用了先前得到的更新门控 $z$ （update gate）。

更新表达式： $h^t = z \odot h^{t-1} + (1 - z)\odot h'$

首先再次强调一下，门控信号（这里的 $z$ ）的范围为0~1。门控信号越接近1，代表”记忆“下来的数据越多；而越接近0则代表”遗忘“的越多。

GRU很聪明的一点就在于，我们使用了同一个门控 $z$ 就同时可以进行遗忘和选择记忆（LSTM则要使用多个门控）。

$z \odot h^{t-1}$ ：表示对原本隐藏状态的选择性“遗忘”。这里的 $z$ 可以想象成遗忘门（forget gate），忘记 $h^{t-1}$ 维度中一些不重要的信息。
$(1-z) \odot h'$ ：表示对包含当前节点信息的 $h'$ 进行选择性”记忆“。与上面类似，这里的 $(1-z)$ 同理会忘记 $h '$ 维度中的一些不重要的信息。或者，这里我们更应当看做是对 $h'$ 维度中的某些信息进行选择。
$h^t = z \odot h^{t-1} + (1 - z)\odot h'$ ：结合上述，这一步的操作就是忘记传递下来的 $h^{t-1}$ 中的某些维度信息，并加入当前节点输入的某些维度信息。