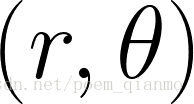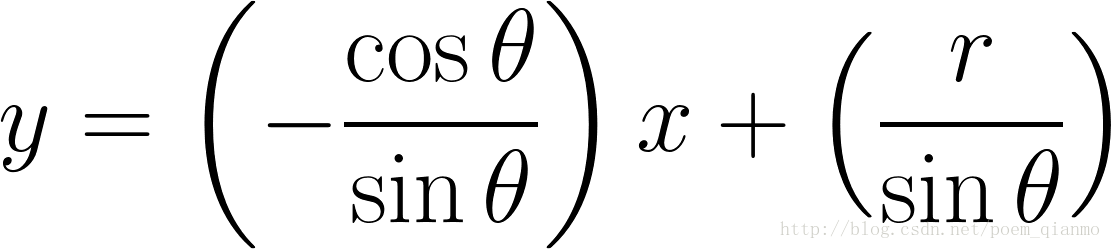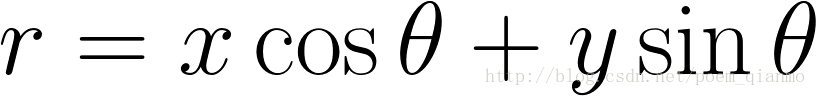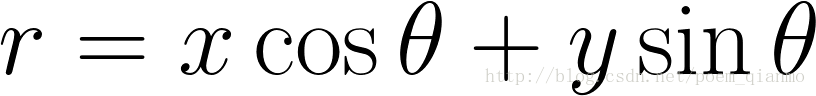简介

• 是一种特征提取技术，该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。
• 最初的设计是用于检测直线和曲线
• 霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值，从而把检测任意形状的问题转化为统计峰值问题。

分类

<1>标准霍夫变换（StandardHough Transform，SHT），由HoughLines函数调用。

<2>多尺度霍夫变换（Multi-ScaleHough Transform，MSHT），由HoughLines函数调用。

<3>累计概率霍夫变换（ProgressiveProbabilistic Hough Transform，PPHT），由HoughLinesP函数调用。

多尺度是经典霍夫变换的一个变种。累计概率霍夫变换是标准霍夫变换的一个改进。

之所以称PPHT为“概率”的，是因为并不将累加器平面内的所有可能的点累加，而只是累加其中的一部分，该想法是如果峰值如果足够高，只用一小部分时间去寻找它就够了。这样猜想的话，可以实质性地减少计算时间。

主要思想

霍夫变换的主要思想是将该方程的参数和变量交换，即用x,y作为已知量k,b作为变量坐标，所以直角坐标系下的直线y=kx+b在参数空间表示为点(k,b)， 而一个点(x1,y1)在直角坐标系下表示为一条直线y1=x1·k+b，其中(k,b)是该直线上的任意点。

为了计算方便，我们将参数空间的坐标表示为极坐标下的γ和θ。因为同一条直线上的点对应的(γ,θ)是相同的，因此可以先将图片进行边缘检测，然后对图像上每一个非零像素点，在参数坐标下变换为一条直线，那么在直角坐标下属于同一条直线的点便在参数空间形成多条直线并内交于一点。因此可用该原理进行直线检测。

原理

直线的表示方式

• 在笛卡尔坐标系: 可由参数: 斜率和截距(m,b) 表示。

• 在极坐标系: 可由参数: 极径和极角表示。

  

  

对于霍夫变换, 我们将采用第二种方式极坐标系来表示直线. 因此, 直线的表达式可为:

化简便可得到:

• 我们可以将通过这个点的一族直线统一定义为:

  

如果对于一个给定点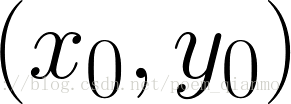我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点X_0= 8 和Y_0= 6 我们可以绘出下图 (在平面):

cv.HoughLinesP

HoughLinesP参数分析

void HoughLinesP(InputArray image,OutputArray lines, double rho, double theta, int threshold, double minLineLength=0,double maxLineGap=0 )

• image为输入图像，要求是单通道，8位图像

• lines为输出参数，4个元素表示，即直线的起始和终止端点的4个坐标（x1,y1）,(x2,y2)

• rho为距离分辨率，一般为1

• heta为角度的分辨率，一般CV_PI/180

• threshold为阈值，hough变换图像空间值最大点，大于则执行

• minLineLength为最小直线长度（像素），即如果小于该值，则不被认为是一条直线

• maxLineGap为直线间隙最大值，如果两条直线间隙大于该值，则被认为是两条线段，否则是一条。

cv.HoughLines

cv2.HoughLines(edges, 1, np.pi/180,200)

1. 第一个参数是输入图像，且必须是二值图像，在进行霍夫变换之前需要采用阈值方法进行边缘检测；
2. 第二和第三个参数分别是r,θ对应的精度；
3. 第四个参数是阈值，判定为直线投票数的最小值；
4. 注意，投票数取决于直线上点的个数，因此这个阈值代表了检测到的直线的最短长度

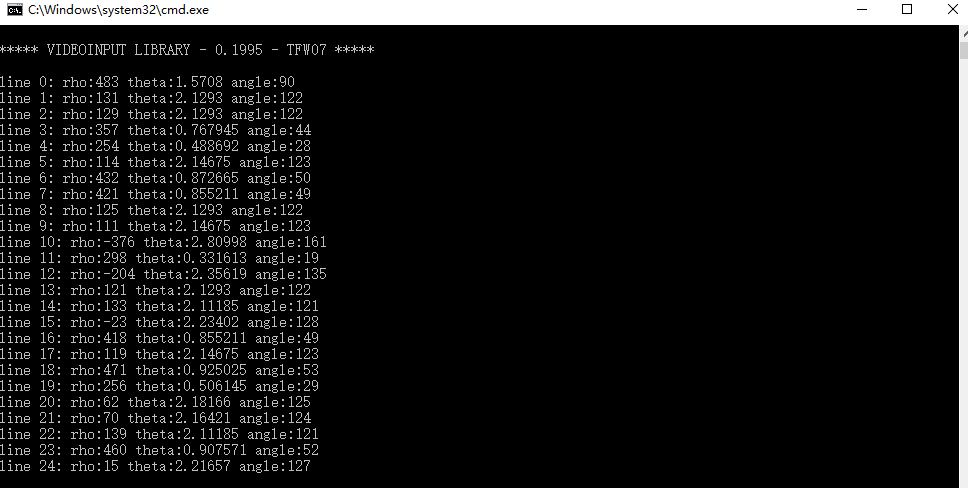
可以看出，转换后的角度范围就是我们想要的度数！值得注意的是，rho表示离坐标原点（就是图片左上角的点）的距离，theta是直线的旋转角度（0度表示垂直线，90度表示水平线）。

例子

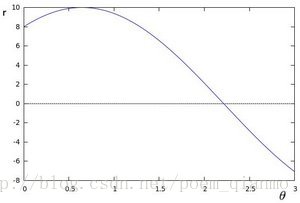
对于原图内任一点(x,y)都可以在参数空间形成一条直线，以图中一条直线为例有参数(γ,θ)=(69.641,30°)，所有属于同一条直线上的点会在参数空间交于一点，该点即为对应直线的参数。

Hough 变换是基于点-线的对偶性思想。

在图像 XY 里，所有过点(x ,y)的直线的方程为

               y = px + q                                (1) 

其中 p 为斜率， q为截距，它也可以改写成如式(2)的形式：

               q = −px+ y                                (2) 

式(2)可以看作为参数空间 PQ 中过点(p ,q)的一条直线。

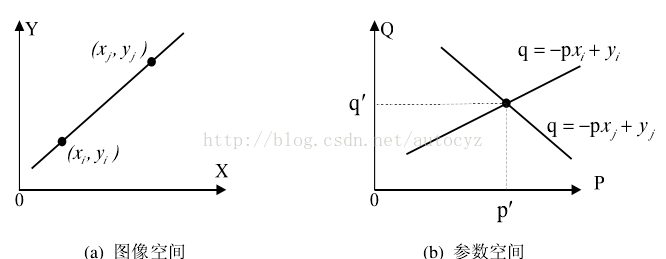
如图下所示，在图像空间中 XY 中过点(xi , yi)的直线方程可以写成yi=pxi+q，也可以写成q=-pxi+yi，后者表示在参数空间PQ中的一条直线。同理对于(xj , yj)也可以写成上式形式。如下图：

​

​ 由此可知，在图像空间中共线的点对应在参数空间里面相交的线，反过来，在参数空间里面相交于同一个点的所有直线在图像空间里面都有共线的点与之对应，这就是点-线的对偶性。

​ Hough 变换就是根据这样的关系把空间里面的检测问题转换到参数空间，通过参数空间里面进行简单的累计统计来完成直线的检测任务。

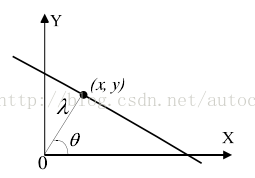
​ 在运算式(2)直线方程时候，如果直线接近竖直方向，则会由于p的值都接近无穷而使得计算量增大，此时我们使用直线的极坐标方程来表示直线，如下图，其方程如式(3) 。

            λ=xcosθ+ysinθ      (3)

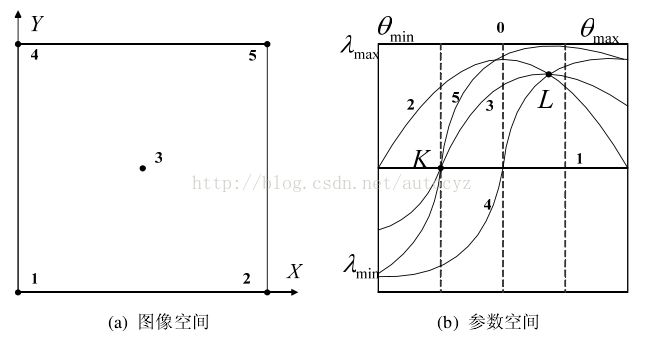
根据这个方程，对于任意一组（λ，θ）都对应一条直线。即原来的点-线对偶性变成了现在的点-正弦曲线对偶性，如图所示，图(a)表示图像空间XY 中的5个点，在图(b)参数空间中对应着5条曲线，这里的θ为[−90 , +90 ]，λ的取值范围为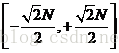， N为图像的宽度。

由图可知，图像空间中各个点可以看作它们在参数空间里面的对应曲线。在图（b）中，曲线 1，3，5 都过 K 点，这表示在图(a)中点 1，3，5 处于同一条直线上，同理，图(a)中点 2，3，4 处于同一条直线上，在图(b)中它们对应的曲线2，3，4 都通过点 L。

Hough 变换的具体实现步骤如下：

(1) 建立一个参数（λ，θ） 空间的二维的数组，该数组相当于一个累加器。

(2) 顺序搜索图像中所有目标(黑色)像素，对于每一个目标像素，在参数空间中根据式(3)找到对应位置，然后在累加器的对应位置加 1。

(3) 求出参数空间(累加器)中最大值，其位置为（λ’，θ’）。

(4) 通过参数空间位置（λ’，θ’） ，根据式(3)找到图像空间中相对应的直线参数。

对于直线hough变换过程，可以这么认为。依次遍历图像的所有像素，对每个像素判断是否满足某个特定条件，若满足，则经过该像素的所有直线区域的计数器加1。为了得到经过某个像素的所有直线区域，可以依次用θ的所有可能取值（例如θ可以以1度为增量，从-90度取到+90度），根据（3）式求出λ的值，从而得到很多组（λ，θ），就对应了所有经过此像素的直线。

例子2

考虑点和线的对应关系，过一点（x1,y1）的直线可表示为：y1=kx1+b，将变量和参数互换，已知一个点(x1,y1),经过这一点的直线簇可以表示为b=(-x1)k+y1。位于同一条直线上的点具有相同的斜率和截距，反映到参数空间上就是这些直线会交于同一点(k,b)。

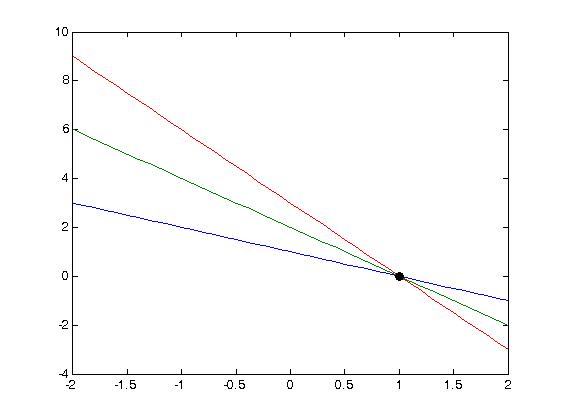
举个例子：图像空间有三个点（1，1），（2，2），（3，3），他们在直线y=1*x+0上，如下图所示

互换参数，在参数空间里这三个点对应三条直线：1=k+b,2=2k+b,3=3k+b，交于同一点（1，0），这一点即图像空间中直线的斜率和截距，如果我们能得到这些点，也就得到了图像空间的直线：

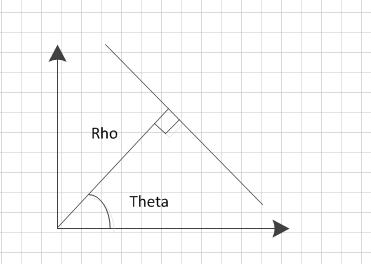
由于上面的变换不能表示斜率为无穷大的情况，因此，采用极坐标的方式：Rho = X * Cos(Theta) + Y * Sin(Theta)：

步骤

在实际操作时，步骤如下：

1、得到图像的边缘信息； 2、对边缘图像中的每一个点，在k-b空间中画出一条直线； 3、对各直线上的点，我们采取“投票”（vote）的方法，即累加：有直线经过这一点，这一点的值加1； 4、遍历k-b空间，找出局部极大值点，这些点的坐标（k，b）就是原图像中可能的直线的斜率和截距。

霍夫变换的计算量和存储都是很大的。

同样的原理，我们可以用来检测圆，等式变为：(x –a ) ^2 + (y-b) ^ 2 = r^2，这样霍夫的参数空间就变成一个三维参数空间。若给定圆的半径则简化为二维霍夫参数空间。

参数

lines = cv.HoughLinesP(threshold_img, 1, np.pi/180, 200)

• 第一个参数是二值化图像，进行霍夫变换之前要进行二值化或者canny边缘检测。
• 第二第三个参数代表ρ和θ的精度。
• 第四个参数是阈值，只有当累加器中的值高于阈值时才被当成是直线。

import cv2
import numpy as np
img = cv2.imread('18.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3)
lines = cv2.HoughLines(edges,1,np.pi/180,200)
for rho,theta in lines[0]:
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a*rho
    y0 = b*rho
    x1 = int(x0 + 1000*(-b))
    y1 = int(y0 + 1000*(a))
    x2 = int(x0 - 1000*(-b))
    y2 = int(y0 - 1000*(a))
    cv2.line(img,(x1,y1),(x2,y2),(0,0,255),2)
cv2.imwrite('houghlines3.jpg',img)

例子3

import cv2
import numpy as np
im = cv2.imread('street.jpg')
im = cv2.GaussianBlur(im, (3,3), 0)
edges = cv2.Canny(im, 50, 150, apertureSize=3)
lines = cv2.HoughLines(edges, 1, np.pi/180, 260)
result = im.copy()
for line in lines[0]:
    rho = line[0]
    theta= line[1]
    if  (theta < (np.pi/4. )) or (theta > (3.*np.pi/4.0)):
        pt1 = (int(rho/np.cos(theta)),0)
        pt2 = (int((rho-result.shape[0]*np.sin(theta))/np.cos(theta)),result.shape[0])
        cv2.line( result, pt1, pt2, (0,0,255))
    else:
        pt1 = (0,int(rho/np.sin(theta)))
        pt2 = (result.shape[1], int((rho-result.shape[1]*np.cos(theta))/np.sin(theta)))
        cv2.line(result, pt1, pt2, (0,0,255), 1)
cv2.imshow('Hough', result)
if cv2.waitKey(0) == 27:
    cv2.destroyAllWindows()

例子4

理解霍夫变换

霍夫变换常用来在图像中提取直线和圆等几何形状，实现原理在维基百科上解释的非常清楚：Hough transform，我来做个简易的解释，感兴趣的可以一看，否则划掉(●ˇ∀ˇ●)：

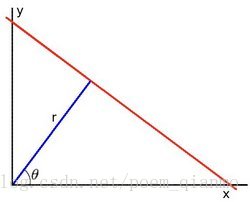
学过几何的都知道，直线可以分别用直角坐标系和极坐标系来表示：

那么经过某个点(x0,y0)的所有直线都可以用这个式子来表示：

也就是说每一个(r,θ)都表示一条经过(x0,y0)直线，那么同一条直线上的点必然会有同样的(r,θ)。如果将某个点所有的(r,θ)绘制成下面的曲线，那么同一条直线上的点的(r,θ)曲线会相交于一点：

OpenCV中首先计算(r,θ) 累加数，累加数超过一定值后就认为在同一直线上（有点拗口，不懂也没关系，暂时会用就行）。

霍夫直线变换

OpenCV中用cv2.HoughLines()在二值图上实现霍夫变换，函数返回的是一组直线的(r,θ)数据：

# 1.加载图片，转为二值图
img = cv2.imread('shapes.jpg')
drawing = np.zeros(img.shape[:], dtype=np.uint8)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray, 50, 150)

# 2.霍夫直线变换
lines = cv2.HoughLines(edges, 0.8, np.pi / 180, 90)

函数中：

• 参数1：要检测的二值图（一般是阈值分割或边缘检测后的图）
• 参数2：距离r的精度，值越大，考虑越多的线
• 参数3：角度θ的精度，值越小，考虑越多的线
• 参数4：累加数阈值，值越小，考虑越多的线

# 3.将检测的线画出来（注意是极坐标噢）
for line in lines:
    rho, theta = line[0]
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a * rho
    y0 = b * rho
    x1 = int(x0 + 1000 * (-b))
    y1 = int(y0 + 1000 * (a))
    x2 = int(x0 - 1000 * (-b))
    y2 = int(y0 - 1000 * (a))

    cv2.line(drawing, (x1, y1), (x2, y2), (0, 0, 255))

统计概率霍夫直线变换

前面的方法又称为标准霍夫变换，它会计算图像中的每一个点，计算量比较大，另外它得到的是整一条线（r和θ），并不知道原图中直线的端点。所以提出了统计概率霍夫直线变换(Probabilistic Hough Transform)，是一种改进的霍夫变换：

drawing = np.zeros(img.shape[:], dtype=np.uint8)
# 3.统计概率霍夫线变换
lines = cv2.HoughLinesP(edges, 0.8, np.pi / 180, 90,
                        minLineLength=50, maxLineGap=10)

前面几个参数跟之前的一样，有两个可选参数：

• minLineLength：最短长度阈值，比这个长度短的线会被排除
• maxLineGap：同一直线两点之间的最大距离

# 3.将检测的线画出来
for line in lines:
    x1, y1, x2, y2 = line[0]
    cv2.line(drawing, (x1, y1), (x2, y2), (0, 255, 0), 1, lineType=cv2.LINE_AA)

cv2.LINE_AA在之前绘图功能中讲解过，表示抗锯齿线型。

霍夫圆变换

霍夫圆变换跟直线变换类似，只不过线是用(r,θ)表示，圆是用(x_center,y_center,r)来表示，从二维变成了三维，数据量变大了很多；所以一般使用霍夫梯度法减少计算量，对该算法感兴趣的同学可参考：Circle Hough Transform

drawing = np.zeros(img.shape[:], dtype=np.uint8)
# 2.霍夫圆变换
circles = cv2.HoughCircles(edges, cv2.HOUGH_GRADIENT, 1, 20, param2=30)
circles = np.int0(np.around(circles))

其中，

• 参数2：变换方法，一般使用霍夫梯度法，详情：HoughModes
• 参数3 dp=1：表示霍夫梯度法中累加器图像的分辨率与原图一致
• 参数4：两个不同圆圆心的最短距离
• 参数5：param2跟霍夫直线变换中的累加数阈值一样

# 将检测的圆画出来
for i in circles[0, :]:
    cv2.circle(drawing, (i[0], i[1]), i[2], (0, 255, 0), 2)  # 画出外圆
    cv2.circle(drawing, (i[0], i[1]), 2, (0, 0, 255), 3)  # 画出圆心

小结

• 霍夫变换用来提取图像中的直线和圆等几何形状
• 霍夫直线变换：cv2.HoughLines()（整条直线）, cv2.HoughLinesP()
• 霍夫圆变换：cv2.HoughCircles()

参考网址

• https://blog.csdn.net/abcjennifer/article/details/7448513
• https://blog.csdn.net/poem_qianmo/article/details/26977557
• https://blog.csdn.net/u014485485/article/details/78608967
• https://blog.csdn.net/tengfei461807914/article/details/77466796