2018-09-18-softmax

2018-09-18 | 阅读：次

一、softmax函数

softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是

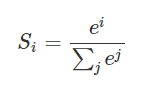
更形象的如下图表示：

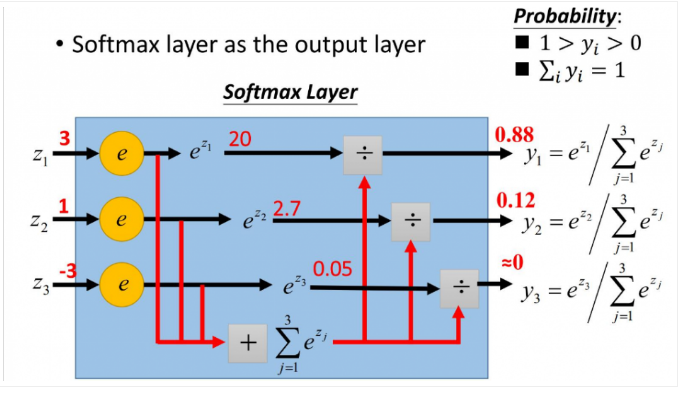
softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

举一个我最近碰到利用softmax的例子：我现在要实现基于神经网络的句法分析器。用到是基于转移系统来做，那么神经网络的用途就是帮我预测我这一个状态将要进行的动作是什么？比如有10个输出神经元，那么就有10个动作，1动作，2动作，3动作…一直到10动作。（这里涉及到nlp的知识，大家不用管，只要知道我现在根据每个状态（输入），来预测动作（得到概率最大的输出），最终得到的一系列动作序列就可以完成我的任务即可）

原理图如下图所示：

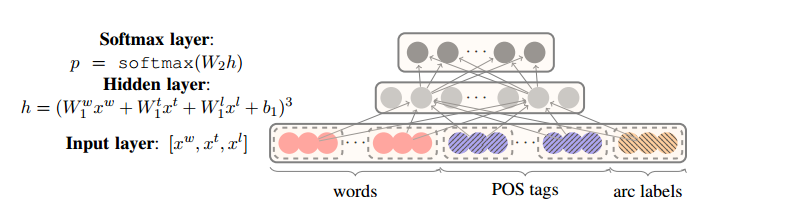
那么比如在一次的输出过程中输出结点的值是如下：

[0.2,0.1,0.05,0.1,0.2,0.02,0.08,0.01,0.01,0.23]

那么我们就知道这次我选取的动作是动作10，因为0.23是这次概率最大的，那么怎么理解多分类呢？很容易，如果你想选取俩个动作，那么就找概率最大的俩个值即可~（这里只是简单的告诉大家softmax在实际问题中一般怎么应用）

二、softmax相关求导

当我们对分类的Loss进行改进的时候，我们要通过梯度下降，每次优化一个step大小的梯度，这个时候我们就要求Loss对每个权重矩阵的偏导，然后应用链式法则。那么这个过程的第一步，就是对softmax求导传回去，不用着急，我后面会举例子非常详细的说明。在这个过程中，你会发现用了softmax函数之后，梯度求导过程非常非常方便！

下面我们举出一个简单例子，原理一样，目的是为了帮助大家容易理解！

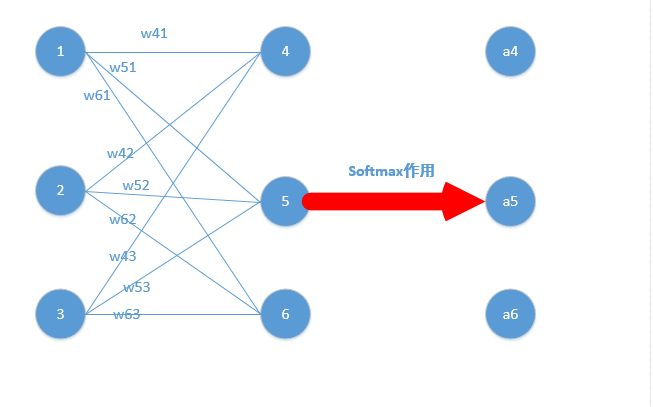
我们能得到下面公式：

z4 = w41o1+w42o2+w43*o3

z5 = w51o1+w52o2+w53*o3

z6 = w61o1+w62o2+w63*o3

z4,z5,z6分别代表结点4,5,6的输出，01,02,03代表是结点1,2,3往后传的输入.

那么我们可以经过softmax函数得到

$a_{4}= \frac{e^{z4} }{z^{z4}+z^{z5}+z^{z6}}$

$a_{5} =\frac{e^{z5} }{z^{z4}+z^{z5}+z^{z6}}$ $a_{6}= \frac{e^{z6} }{z^{z4}+z^{z5}+z^{z6}}$

好了，我们的重头戏来了，怎么根据求梯度，然后利用梯度下降方法更新梯度！要使用梯度下降，肯定需要一个损失函数，这里我们使用交叉熵作为我们的损失函数，为什么使用交叉熵损失函数，不是这篇文章重点，后面有时间会单独写一下为什么要用到交叉熵函数（这里我们默认选取它作为损失函数）

交叉熵函数形式如下：

$Loss = -\sum_{i}^{}{y_{i}lna_{i} }$

其中y代表我们的真实值，a代表我们softmax求出的值。i代表的是输出结点的标号！在上面例子，i就可以取值为4,5,6三个结点（当然我这里只是为了简单，真实应用中可能有很多结点）

现在看起来是不是感觉复杂了，居然还有累和，然后还要求导，每一个a都是softmax之后的形式！

但是实际上不是这样的，我们往往在真实中，如果只预测一个结果，那么在目标中只有一个结点的值为1，比如我认为在该状态下，我想要输出的是第四个动作（第四个结点）,那么训练数据的输出就是a4 = 1,a5=0,a6=0，哎呀，这太好了，除了一个为1，其它都是0，那么所谓的求和符合，就是一个幌子，我可以去掉啦！

为了形式化说明，我这里认为训练数据的真实输出为第j个为1，其它均为0！

那么Loss就变成了 $Loss = -y_{j}lna_{j}$ ,累和已经去掉了，太好了。现在我们要开始求导数了！

我们在整理一下上面公式，为了更加明白的看出相关变量的关系：

其中 $y_{j} =1$ ,那么形式变为 $Loss = -lna_{j}$

那么形式越来越简单了，求导分析如下：

参数的形式在该例子中，总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.这些，那么比如我要求出w41,w42,w43的偏导，就需要将Loss函数求偏导传到结点4，然后再利用链式法则继续求导即可，举个例子此时求w41的偏导为:

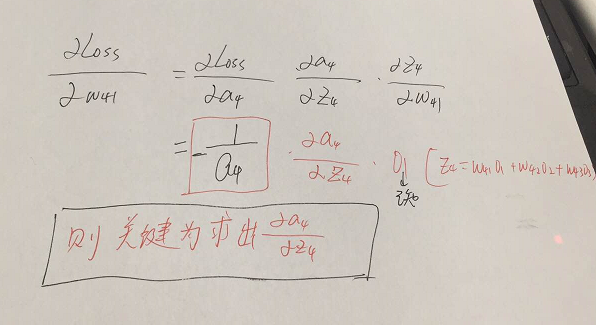
w51…..w63等参数的偏导同理可以求出，那么我们的关键就在于Loss函数对于结点4,5,6的偏导怎么求，如下：

这里分为俩种情况：

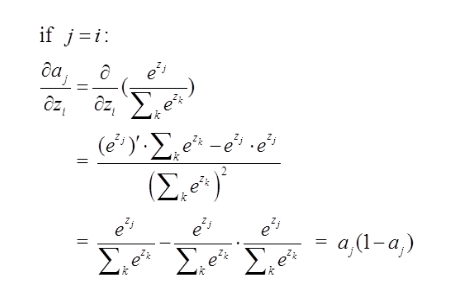
j=i对应例子里就是如下图所示：

比如我选定了j为4，那么就是说我现在求导传到4结点这！

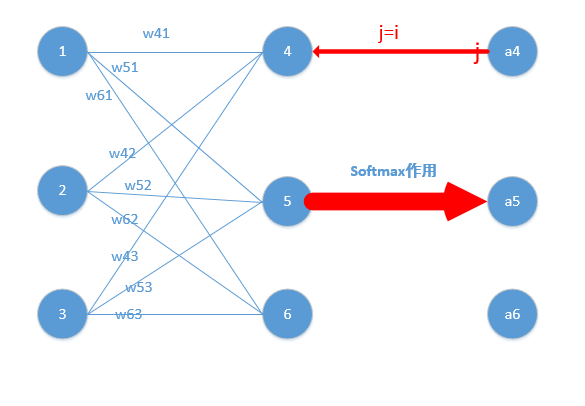
那么由上面求导结果再乘以交叉熵损失函数求导

$Loss = -lna_{j}$ ，它的导数为 $-\frac{1}{a_{j} }$ ,与上面 $a_{j}(1-a_{j} )$ 相乘为 $a_{j}-1$ （形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果减1即可，后面还会举例子！）那么我们可以得到Loss对于4结点的偏导就求出了了（这里假定4是我们的预计输出）

第二种情况为：

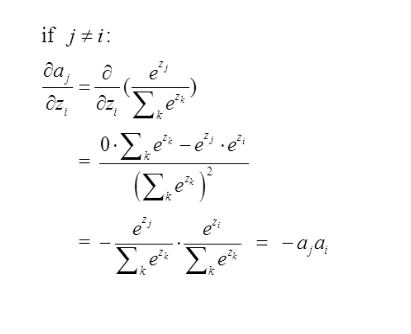
这里对应我的例子图如下，我这时对的是j不等于i，往前传：

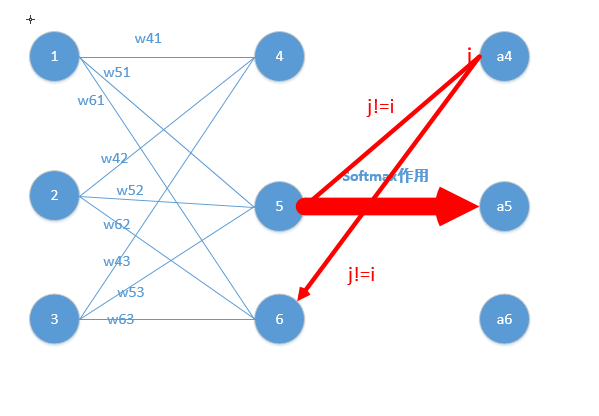
那么由上面求导结果再乘以交叉熵损失函数求导

$Loss = -lna_{j}$ ，它的导数为 $-\frac{1}{a_{j} }$ ,与上面 $-a_{j}a_{i}$ 相乘为 $a_{i}$ （形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果保存即可，后续例子会讲到）这里就求出了除4之外的其它所有结点的偏导，然后利用链式法则继续传递过去即可！我们的问题也就解决了！

背景与定义

在Logistic regression二分类问题中，我们可以使用sigmoid函数将输入 $Wx + b$ 映射到 $(0, 1)$ 区间中，从而得到属于某个类别的概率。将这个问题进行泛化，推广到多分类问题中，我们可以使用softmax函数，对输出的值归一化为概率值。

这里假设在进入softmax函数之前，已经有模型输出 $C$ 值，其中 $C$ 是要预测的类别数，模型可以是全连接网络的输出 $a$ ，其输出个数为 $C$ ，即输出为 $a_{1}, a_{2}, ..., a_{C}$ 。

所以对每个样本，它属于类别 $i$ 的概率为：

$y_{i} = \frac{e^{a_i}}{\sum_{k=1}^{C}e^{a_k}} \ \ \ \forall i \in 1...C$

通过上式可以保证 $\sum_{i=1}^{C}y_i = 1$ ，即属于各个类别的概率和为1。

导数

对softmax函数进行求导，即求

$\frac{\partial{y_{i}}}{\partial{a_{j}}}$

第 $i$ 项的输出对第 $j$ 项输入的偏导。代入softmax函数表达式，可以得到：

$\frac{\partial{y_{i}}}{\partial{a_{j}}} = \frac{\partial{ \frac{e^{a_i}}{\sum_{k=1}^{C}e^{a_k}} }}{\partial{a_{j}}}$

用我们高中就知道的求导规则：对于

$f(x) = \frac{g(x)}{h(x)}$

它的导数为

$f'(x) = \frac{g'(x)h(x) - g(x)h'(x)}{[h(x)]^2}$

所以在我们这个例子中，

$g(x) = e^{a_i} \ h(x) = \sum_{k=1}^{C}e^{a_k}$

上面两个式子只是代表直接进行替换，而非真的等式。

$e^{a_i}$ （即 $g(x)$ ）对 $a_j$ 进行求导，要分情况讨论：

如果 $i = j$ ，则求导结果为 $e^{a_i}$
如果 $i \ne j$ ，则求导结果为 $0$

再来看 $\sum_{k=1}^{C}e^{a_k}$ 对 $a_j$ 求导，结果为 $e^{a_j}$ 。

所以，当 $i = j$ 时：

$\frac{\partial{y_{i}}}{\partial{a_{j}}} = \frac{\partial{ \frac{e^{a_i}}{\sum_{k=1}^{C}e^{a_k}} }}{\partial{a_{j}}}= \frac{ e^{a_i}\Sigma - e^{a_i}e^{a_j}}{\Sigma^2}=\frac{e^{a_i}}{\Sigma}\frac{\Sigma - e^{a_j}}{\Sigma}=y_i(1 - y_j)$

当 $i \ne j$ 时：

$\frac{\partial{y_{i}}}{\partial{a_{j}}} = \frac{\partial{ \frac{e^{a_i}}{\sum_{k=1}^{C}e^{a_k}} }}{\partial{a_{j}}}= \frac{ 0 - e^{a_i}e^{a_j}}{\Sigma^2}=-\frac{e^{a_i}}{\Sigma}\frac{e^{a_j}}{\Sigma}=-y_iy_j$

其中，为了方便，令 $\Sigma = \sum_{k=1}^{C}e^{a_k}$

对softmax函数的求导，我在两年前微信校招面试基础研究岗位一面的时候，就遇到过，这个属于比较基础的问题。

softmax的计算与数值稳定性

在Python中，softmax函数为：

def softmax(x):
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x)

传入[1, 2, 3, 4, 5]的向量

>>> softmax([1, 2, 3, 4, 5])
array([ 0.01165623,  0.03168492,  0.08612854,  0.23412166,  0.63640865])

但如果输入值较大时：

>>> softmax([1000, 2000, 3000, 4000, 5000])
array([ nan,  nan,  nan,  nan,  nan])

这是因为在求exp(x)时候溢出了：

import math
math.exp(1000)
# Traceback (most recent call last):
#   File "<stdin>", line 1, in <module>
# OverflowError: math range error

一种简单有效避免该问题的方法就是让exp(x)中的x值不要那么大或那么小，在softmax函数的分式上下分别乘以一个非零常数：

$y_{i} = \frac{e^{a_i}}{\sum_{k=1}^{C}e^{a_k}}= \frac{Ee^{a_i}}{\sum_{k=1}^{C}Ee^{a_k}}= \frac{e^{a_i+log(E)}}{\sum_{k=1}^{C}e^{a_k+log(E)}}= \frac{e^{a_i+F}}{\sum_{k=1}^{C}e^{a_k+F}}$

这里 $log(E)$ 是个常数，所以可以令它等于 $F$ 。加上常数 $F$ 之后，等式与原来还是相等的，所以我们可以考虑怎么选取常数 $F$ 。我们的想法是让所有的输入在0附近，这样 $e^{a_i}$ 的值不会太大，所以可以让 $F$ 的值为：

$F = -max(a_1, a_2, ..., a_C)$

这样子将所有的输入平移到0附近（当然需要假设所有输入之间的数值上较为接近），同时，除了最大值，其他输入值都被平移成负数， $e$ 为底的指数函数，越小越接近0，这种方式比得到nan的结果更好。

def softmax(x):
    shift_x = x - np.max(x)
    exp_x = np.exp(shift_x)
    return exp_x / np.sum(exp_x)

>>> softmax([1000, 2000, 3000, 4000, 5000])
array([ 0.,  0.,  0.,  0.,  1.])

当然这种做法也不是最完美的，因为softmax函数不可能产生0值，但这总比出现nan的结果好，并且真实的结果也是非常接近0的。

三、下面我举个例子来说明为什么计算会比较方便，给大家一个直观的理解

举个例子，通过若干层的计算，最后得到的某个训练样本的向量的分数是[ 2, 3, 4 ], 那么经过softmax函数作用后概率分别就是=[ $\frac{e^{2} }{e^{2}+e^{3}+e^{4}}$ , $\frac{e^{3} }{e^{2}+e^{3}+e^{4}}$ , $\frac{e^{4} }{e^{2}+e^{3}+e^{4}}$ ] = [0.0903,0.2447,0.665],如果这个样本正确的分类是第二个的话，那么计算出来的偏导就是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]，是不是非常简单！！然后再根据这个进行back propagation就可以了

四、建立一个softmax模型

Placeholders

我们通过创建输入图片和目标输出类别的节点来开始构建计算图。

x = tf.placeholder(tf.float32, shape=[None, 784])
y_ = tf.placeholder(tf.float32, shape=[None, 10])

这里x和y_不是特定的值。相反，它们各自是一个占位符 — 当我们要求TensorFlow运行计算时，我们将输入一个值。

输入图片x将由2维浮点数张量组成。这里，我们赋给它一个为[None, 784]的形状 ，其中784是单个平坦化28乘28像素MNIST图像的维数，None表示对应于批量大小的第一维可以是任何大小。目标输出类别y_也将由二维张量组成，其中每行是一个one-hot 10维向量，指示对应的MNIST图像属于哪个数字类别（零到九）。

变量

我们现在为我们的模型定义权重W和偏置b。我们可以想象，像其他输入一样处理这些信息，但是TensorFlow有一个更好的处理方式：Variable。一个Variable是位于TensorFlow计算图中的一个值。它可以被使用，甚至被计算修改。在机器学习应用中，人们通常让模型的参数为Variable。

W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))

我们将调用中每个参数的初始值传递给tf.Variable。在这种情况下，我们将W和b初始化为满零的张量。 W是一个784x10矩阵（因为我们有784个输入特征和10个输出），而b是一个10维向量（因为我们有10个类别）。

在变量可以在会话中使用之前，它们必须使用该会话进行初始化。这一步将获得已经指定的初始值（在这种情况下，张量满了零），并将它们分配给每个变量。这可以一次完成所有变量：

sess.run(tf.global_variables_initializer())

预测的类别和损失函数

我们现在可以实现我们的回归模型。它只需要一行！我们将向量化的输入图片x乘以权重矩阵W，添加偏置b。

y = tf.matmul(x,W) + b

我们可以轻松地指定一个损失函数。损失表明模型在一个样本上的预测有多糟糕；在这些样本之间训练时我们尝试尽量减少所有这些样本的损失。在这里，我们的损失函数是目标和应用于模型预测的softmax激活函数之间的交叉熵。和初学者教程一样，我们使用稳定公式：

cross_entropy = tf.reduce_mean(
    tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))

请注意，tf.nn.softmax_cross_entropy_with_logits内部将softmax用于模型的非归一化预测结果并对类别求和，tf.reduce_mean取所有这些和的平均值。

训练模型

现在我们已经定义了我们的模型和训练损失函数，使用TensorFlow进行训练非常简单。因为TensorFlow知道整个计算图，它可以使用自动微分来找出相对于每个变量的损失的梯度。 TensorFlow有多种内置优化算法。对于这个例子，我们将使用最陡的梯度下降，步长为0.5，下降交叉熵。

train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

TensorFlow实际上在这一行中做了什么是为计算图添加新的操作。这些操作包括计算梯度，计算参数更新步骤以及将更新步骤应用于参数。

返回的操作train_step，在运行时，将梯度下降更新应用于参数。 训练模型可以通过重复运行train_step来完成。

for _ in range(1000):
  batch = mnist.train.next_batch(100)
  train_step.run(feed_dict={x: batch[0], y_: batch[1]})

我们在每次训练迭代中加载100个训练样例。然后我们使用feed_dict运行操作，并用feed_dict以训练样本替换placeholder张量x和y_。请注意，你可以使用feed_dict替换计算图中的任何张量 — 不仅限于placeholder。

stone

Linxia Yao

2018-09-18-softmax

一、softmax函数

二、softmax相关求导

背景与定义

导数

softmax的计算与数值稳定性

三、下面我举个例子来说明为什么计算会比较方便，给大家一个直观的理解

四、建立一个softmax模型

Placeholders

变量

预测的类别和损失函数

训练模型

一、softmax函数

二、softmax相关求导

背景与定义

导数

softmax的计算与数值稳定性

三、下面我举个例子来说明为什么计算会比较方便，给大家一个直观的理解

四、 建立一个softmax模型

Placeholders

变量

预测的类别和损失函数

训练模型

四、建立一个softmax模型